이것도 영상편집이 안끝나 그냥 올립니다.
영상기획서
SLT
|
제목 |
막의 진동 형상과 원리 탐구 |
||
|
유튜브 제목 |
공돌이 용달이 실험했던 바이올린 활, Hz별로 알아봤습니다 |
||
|
작성일시 |
|
분과 |
물리 |
|
작성자 |
김민성, 류관형 |
비용 |
0 |
영상 순서(순서대로 번호를 넣고, 안넣을 경우 x 표시)
|
컨텐츠 |
미리보기 |
인트로 |
실험과정 |
결과 |
설명 |
데이터 분석 |
결론 |
|
번호 |
1 |
2 |
|
4 |
3, 5 |
|
|
인트로
|
대사: 방금 보신 모양을 클라드니 도형이라 하고, 저 실험을 막의 진동이라 하며, 이는 막에서 정상파의 합으로 이루어집니다. 안녕하세요 연구노트의 관형입니다. 오늘은 조금 평범한 실험을 준비했는데요, 이 실험을 이해하기 위해서, 정상파에 대한 설명부터 듣고 실제 Hz별로 모양이 어떻게 생겨나는지 관찰한 다음, 정상파를 활용하는 막의 진동에 대해 알아보죠. |
설명
|
설명 keypoint: |
|
|
스크립트(그림 그리기 전에 쓰기) |
그림 그려야 하는 것 |
|
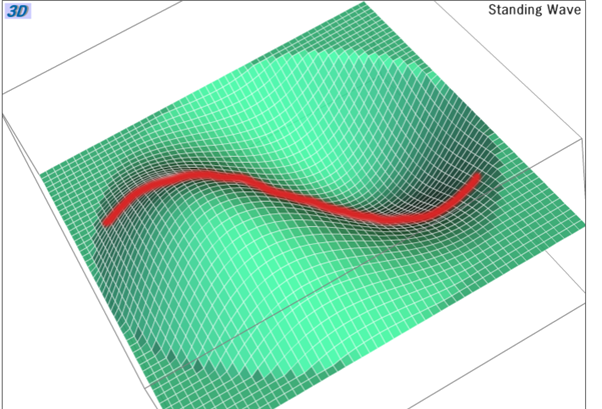
여러분들은 줄넘기를 길게 늘려서 친구와 흔들어 본적이 있을 것입니다. 흔들다 보면 줄이 제자리에서 흔들리는 것 처럼 보일 때가 있는데, 이때 이 파동을 정상파라고 합니다. (움짤)진동의 배와 마디의 위치가 공간적으로 이동하지 않는 파동입니다. 파동의 진폭이 0일때의 위치를 마디라고 하고 진폭이 최대가 되는 위치를 배라고 합니다. 정상파는 같은 진폭과 파장, 진동수를 가지고 y₁=A sin (kx-t)와 y₂=A sin (kx+t)의 파동함수를 가지는 횡파가 마주보며 진행할 때 생기는 파동을 말합니다. (그림)중첩의 원리란, 두개 이상의 파동이 진행중에 만나면 파동들의 변위가 합성되어 모양이 변하는것인데, 이 중첩의 원리에 의해 두 파동함수의 변위인 진폭을 합성하면 y=y1+y2=A sin (kx-t) +A sin (kx+t)가 되고 삼각함수 항등식을 이용하면 y=(2Asin kx) cos t의 정상파 파동함수를 나타냅니다. 정상파의 파동함수에서 진폭인 sin kx=0을 만족하는 점들을 마디라고 하고 sin kx=1을 만족하는 위치를 배라고 합니다. 즉, 마디의 위치는 x=0,2,,32,...=n2 n=0,1,2,3,...이고 배의 위치는 x=4,34,54,...=n4 n=1,3,5,...이 주어집니다
|
줄넘기 돌리는거 측면 그 사진에서 마디와 배 표시 수식 수식에 진폭, 파장, 진동수 설명 표시 파동함수 시각화 파동함수 두 개의 중첩을 화살표로 표시 정상파 움짤 10초 건너뛰기-유도과정 생략 수식 또 수식 모드에 따른 정상파 그리고 마디와 배의 위치 표시 |
결과
|
산출된 데이터: 사각 판에서 모래의 모양 |
|
|
화면 구성(그림) |
보여줄 형식 |
|
아래에 Hz 영상과 동기화 시켜 내보내기 |
결과값 중 보여줄 것을 택하여 일정 형식으로 넣어주세요 독립/종속 변수, 측정값 등 n회 시행에 n번씩 등 |
|
대사: 저 조절기구는 직류를 Hz를 다르게 할 수 있는 교류로 바꿔서, 파원에서 만드는 진동의 직접적인 에너지를 전달합니다. 그럼 0부터 800Hz까지 바꿀 수 있는데요, 그 값들을 조정하면서 어떤 도형이 생기는지 관찰해봅시다. |
|
설명
|
설명 keypoint: |
|
|
스크립트(그림 그리기 전에 쓰기) |
그림 그려야 하는 것 |
|
원형 막에서 저러한 현상이 일어나는 이유는 정상파가 원형 내부에 갇히게 되는데, 막에서의 파동은 2차원 파동이므로 닫힌도형의 내부에서는 도형의 경계 모양에 따른 정상파가 만들어집니다. 줄에서 처럼 일차원 파동의 마디는 점인 반면에 (그림0)이차원 파동인 막의 경우, 그림에 나온 것 처럼 파동이 억제되어 있는 마디는 곡선의 모양을 할 것입니다. 원형 막의 경우에는 경계를 따라 원형의 마디선이 만들어지고 그 내부에서도 원을 분할하는 곡선이나 직선의 마디선이 만들어져서 (그림1) 그림처럼 훨씬 다양하고 복잡한 상태가 있을 수 있습니다. 그림에서 푸른 색부분이 올라올때는 붉은부분이 밑으로 내려가고, 마찬가지로 사각 막에서도 생각 해보면 (그림2) 화면의 그림처럼 나타납니다.
|
원형(45도 기울여서) 에 수직하는 정상파 도형의 경계에 따라 정상파가 결정(텍스트 및 화살표 등) 그림0 파원과 원형 막, 이에 따른 마디 클라드니 도형 그림에서 마디선 표시(화살표) 사각판에서의 클라드니 자료 |




데이터 분석
|
분석 대상 |
과정 |
결과물 |
|
Hz와 모래의 진동 |
웹에서의 클라드니 도형과 비교 |
|
|
대사: 다음은 실제 클라드니 도형이라 불리는 그림과 실험결과를 비교한 모습입니다. 완벽한 사각형의 철판은 아니기에 차이는 있을 수 있지만 같은 Hz에서 비슷한 모양을 나타냄을 알 수 있습니다. 이 실험을 유체에서도 똑같이 할 수 있을까요? 다음 영상에 실험결과가 올라갑니다. 감사합니다. |
||
미리보기
|
(구체적인 부분 표시, 3~4초 내) 결과화면 약간 보여주기(클라드니 도형 나타나게) |
출처표기 안한거 불편한건 나뿐인가...? 부원들,,, 내가 그렇게 말해도,,
'프로젝트 > 아카이브' 카테고리의 다른 글
| 11회 수학체험전 책 표지 및 홍보 포스터 (0) | 2020.03.01 |
|---|---|
| 2학년 제주도 자연탐사 포스터 (0) | 2020.03.01 |
| 롤러코스터 영상 기획자료 (0) | 2020.02.15 |
| 슐리렌 장치 영상 기획자료 (11) | 2020.02.15 |
| 유튜브 미리보기 편집본들 (0) | 2020.02.15 |
